KÜMELERDE İŞLEMLER
a) Birleşim İşlemi
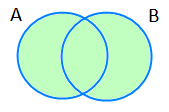
A kümesi ile B kümesinin bütün elemanlarından oluşan kümeye, bu iki kümenin birleşimi denir.
A ⪠B şeklinde gösterilir. A ⪠Bkümesi aşağıdaki şekildeki taralı bölgedir.
Kümelerde birleşim ile ilgili özellikler;
A ⪠A = A (Tek kuvvet özelliği)
A âª Ø = A
A ⪠E = E
A ⪠B = B ⪠A (Değişme özelliği)
(A ⪠B) ⪠C = A ⪠(B ⪠C) (Birleşme özelliği)
A ⪠B = Ø ise A = Ø ve B = Ø dir.
A â B ise A ⪠B = B dir.
b) Kesişim İşlemi
A kümesi ile B kümesinin ortak elemanlarından oluşan kümeye, bu iki kümenin kesişimi denir.
A â© B şeklinde gösterilir.A â© B kümesi taralı bölgedir.
Kümelerde kesişim ile ilgili özellikler;
A â© A = A dır. (Tek kuvvet özelliği)
A â© Ø = Ø â© A = Ø
A â© E = E â© A = A
A â© B = B â© A (Değişme özelliği)
(A â© B) â© C = A â© (B â© C) (Birleşme özelliği)
A ⪠(B â© C) = (A ⪠B) â© (A ⪠C) (Birleşimin kesişim üzerine dağılma özelliği)
A â© (B ⪠C) = (A â© B) ⪠(A â© C) (Kesişimin birleşim üzerine dağılma özelliği)
A â B ? A â© B = A
A ? Ø ve B ? Ø olmak üzere,
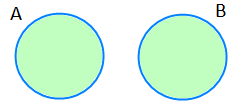
A â© B = Ø ise A ile B kümelerine ayrık kümeler denir.
A ile B ayrık kümeler
s(A ⪠B) = s(A) + s(B) s(A ⩠B)
s(A ⪠B ⪠C) = s(A) + s(B) + s(C) s(A ⩠B) s(A ⩠C) s(B ⩠C) + s(A ⩠B ⩠C)
c) Tümleme İşlemi
E, evrensel küme ve A â E olsun.
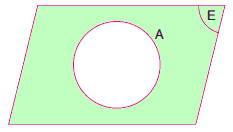
Evrensel kümede olan fakat A kümesinde olmayan bütün elemanların oluşturduğu kümeye A nın tümleyeni denir ve Aı ile gösterilir.
Taralı bölge A kümesinin tümleyenidir.
A â© Aı = Ø
A ⪠Aı = E
Øı = E, Eı = Ø
(Aı)ı = A
s(A) + s(Aı) = s(E)
A â B ? Bı â Aı
(A ⪠B)ı = Aı â© Bı (De Morgan kuralı)
(A â© B)ı = Aı ⪠Bı (De Morgan kuralı)
d) Fark İşlemi
A ve B herhangi iki küme olsun. A kümesinin elemanları içinden varsa B kümesinin elemanları çıkarılarak elde edilen kümeye A fark B kümesi denir ve A \ B ya da A B şeklinde gösterilir.
A A = Ø
E A = Aı
A B = A â© Bı
A ? B ise A B ? B A
A Ø = A, Ø A = Ø
(A B) ⪠B = A ⪠B
(A B) C = A (B ⪠C)
KÜMELERDEKİ İŞLEMLERLE PROBLEM ÇÖZÜMÜ
Yukarıdaki venn şemasında Almanca bilenlerin kümesi A, Fransızca bilenlerin kümesi F ile gösterilmiştir.
Almanca bilenlerin sayısı s(A) = x + y
Fransızca bilenlerin sayısı s(F) = y + z
Almanca bilmeyenlerin sayısı s(Aı) = t + z
Fransızca bilmeyenlerin sayısı s(Fı) = x + t
Almanca ve Fransızca bilenlerin sayısı s(A â© F) = y
Almanca veya Fransızca bilenlerin sayısı s(A ⪠F) = x+y+z
Almanca bilip, Fransızca bilmeyenlerin sayısı s(A F) = x
Fransızca bilip, Almanca bilmeyenlerin sayısı; s(F A) = z
Yalnız bir dil bilenlerin sayısı; s(A F) + s(F A) = x + z
Bu dillerin hiçbirini bilmeyenlerin sayısı, s(A ⪠F)ı = t
Bu iki dilden en az birini bilenlerin sayısı; s(AâªF)= x+y+z
Bu iki dilden en çok birini bilenlerin sayısı; s(A â© F)ı = x+z+t dir.









 Alıntı ile Cevapla
Alıntı ile Cevapla