Parabol Konu Anlatımı
Bu derste parabol konusu ilgili bilmemiz gerekenleri baştan sona ele alacağız. İkinci dereceden bir denklem koordinat sistemi üzerine aktarıldığında parabol ortaya çıkar.
İkinci dereceden denklemler f(x) = ax2 + bx + c formundadır. Bir parabolün denklemi de bu şekilde olur.
Grafiksel olarak birinci dereceden denklemler doğrusal olarak ifade edilir. Bir denklem doğru denklemiise o denklem birinci dereceden olmak zorundadır. Birinci dereceden denklem demek x üssü 1'den büyük olan ifade içermiyor demektir.
- F(x) = 3x + 4
- F(x) = -2x
- F(x) = -7x - 4
Yukarıdaki denklemlerin hepsi birinci dereceden denklemlerdir. Bu da bir doğru denklemi demektir.
İkinci dereceden denklemlere geldiğimiz zaman durum değişir. Grafikte gördüğümüz şekil parabolik olur. Parabolik grafikler doğrusal değil eğriseldir.
İkinci Dereceden Fonksiyonlar
Parabolün diğer adı ikinci dereceden fonksiyonlardır. Bir fonksiyon ikinci derecedense grafiği parabol olur.
- y = 3x3 + 2x2 + 3
- y = x2 - 2
- y = x - 4
- y = x4 - x2 - 12
Yukarıdaki fonksiyonlardan hangileri ikinci derecedendir?
Doğru bildiniz. Sadece 2 numaralı fonksiyon ikinci derecedendir. İkinci dereceden fonksiyonlarda mutlaka x2 teriminin olması gerekir.
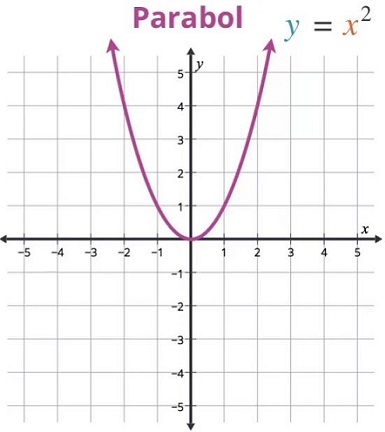
İkinci dereceden fonksiyonların en basiti y = x2 fonksiyonudur. Bu fonksiyonun oluşturduğu parabol bilinmelidir.
Yukarıda ilk parabolümüzün çizimini görüyoruz. Görüldüğü gibi parabol x eksenini 0 noktasından kesiyor. Öyleyse bu denklemin tek bir kökü vardır o da 0'dır. Değip geçme şeklinde değil teğet kesme durumu var. Öyleyse 0 çift katlı bir denklem köküdür.
Parabol konusunu çalışırken her zaman ax2 + bx + c formatını aklınızda bulundurun. Ayrıca a, b ve c katsayıları parabolün özelliklerini bilmemiz açısından bize çok önemli bilgiler verecektir.
Bir parabol grafiğiyle ilgili kontrol etmemiz gereken bilgiler şunlardır:
- Parabolün kolları aşağı mı yukarı mı bakıyor?
- Parabol x eksenini hangi noktalardan kesiyor?
- Parabol y eksenini hangi noktadan kesiyor?
- Parabolün tepe noktası hangi noktada yer alıyor?
Bu bilgiler ışığında parabolle ilgili her şeyi ortaya koyabiliriz. Grafikten denklemi, denklemden ise grafiği elde edebiliriz.
Fonksiyonda x2'nin katsayısı olan a pozitifse grafiğin kolları yukarı doğrudur.
Yukarıda verdiğimiz x2 parabolünde a katsayısı 1 yani pozitif olduğu için denklem kolları yukarıya bakar.
Parabolün Y Eksenini Kestiği Nokta
Parabolün y ekseni hangi noktada kestiği bizim için önemli bir bilgidir.
Y ekseni fonksiyonun değer kümesini yansıtır. Yani fonksiyonda x yerine yazdığınız her değerin görüntüsü y'deki değere karşılık gelir. Parabolün grafikte y eksenini kestiği noktayı bulmak için x yerine 0 yazmak gerekir. Çünkü y ekseni üzerinde x = 0 olur.
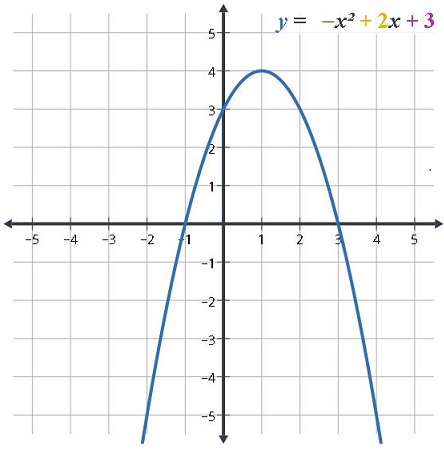
Yukarıdaki grafikteki parabolün denklemi -x2 + 2x + 3 şeklindedir. Grafikte y'yi kesen noktayı bulmak için x'e 0 değerini verdiğimizde 3 sonucunu buluruz. Bu da şekilde görüldüğü gibi y ekseninin kesildiği noktadır.
Grafiğin y eksenini kestiği nokta denklemdeki c katsayısına eşittir. Eğri mutlaka y eksenini kesecektir. Eğer c = 0 olursa parabol eğrisi koordinat sistemini 0 noktası olan orjinde kesecektir.
İkinci Dereceden Fonksiyonun Kökleri
Parabol ikinci dereceden fonksiyonun koordinat sistemine aktarılmış şeklidir dedik. Denklemler konusundan biliyoruz ki ikinci dereceden denklemlerin 2 tane kökü olur.
Bir denklemin kökü onu 0'a eşitleyen değerdir. Parabol üzerinde görüntü kümesi olan y'nin 0 olduğu değerlere baktığımız zaman x eksenini görürüz. Öyleyse bir denklemin kökleri o denklemin parabolünün x eksenini kestiği noktalardır diyebiliriz.
Yukarıdaki parabol x eksenini -1 ve 3 apsisli noktalarda kesmektedir. Öyleyse bu parabolün kökleri de -1 ve 3 olur.
Parabol x eksenini kesmiyorsa?
Yukarıda parabol y eksenini mutlaka keser dedik ama parabol x eksenini kesmeyebilir. Böyle bir durumda denklemin reel sayılarda çözüm kümesi yoktur deriz. Hatırlarsanız ikinci dereceden denklemlerde Î < 0 olduğunda böyle bir durum ortaya çıkmaktaydı.
Parabol x eksenine teğetse denklemin çift katlı tek bir kökü var demektir.
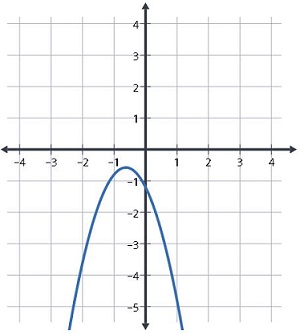
Yukarıdaki parabol örneğinde eğirinin x eksenine değmediğini görüyoruz. Öyleyse bu fonksiyonun reel sayılarda kökü yoktur.
Parabolün Tepe Noktası
Parabolün kıvrım alıp tekrar yön aldığı zirve noktasına tepe noktası denir. Kolları yukarı doğru olan parabolde tepe noktası en küçük nokta iken kolları aşağı doğru olan parabolde ise en yüksek noktadır.
Parabol sorularında karşımıza denklemin en küçük noktası diyorsa kollar yukarı doğru bir parabol vardır karşımızda (a > 0), eğer denklemin alabileceğin en yüksek değer tarzı bir ifade içeriyorsa yine tepe noktasını bulmamız gerekir (a < 0).
Parabolün tepe noktası bir nokta olduğunu göre bu noktanın bir apsis (x) bir de ordinat (y) değeri olacaktır. Öyleyse tepe noktasını T(r, k) olarak ifade edebiliriz.
İkinci dereceden bir denklemin tepe noktasının apsis değerini (r) bulup bunu denklem içerisinde yerine yazarsak ordinat (k) değerini de buluruz.
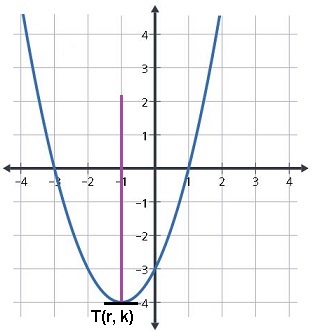
Yukarıdaki görselde örnek bir parabol grafiği verilmiştir. Parabol grafiklerinin simetrik olduğuna dikkat ediniz. Tepe noktasını kesecek bir doğru parçası çizdiğimizde doğru parçasının sağ ve sol yanı simetrik olmaktadır. Bu nedenle tepe noktası denklemin iki kökünün tam orta hizasında bulunmaktadır.
Yukarıdaki parabolün kökleri -3 ve 1'dir. Bu iki değerin aritmetik ortalaması (ortalama noktası) ise -1 olmaktadır. Öyleyse parabolün tepe noktasının apsisi (r) şekilde de görüldüğü gibi -1 olur.
İkinci dereceden bir denklemin kökler toplamını bulurken -b/a formülünü kullanıyorduk. Burada aritmetik ortalama aldığımız için kökler toplamının yarısını alırız. Öyleyse tepe noktasının apsisi -b/2a formülüyle elde edilebilir.
Parabolün tepe noktasının ordinatı resimde görüldüğü gibi -4'tür. Ancak grafikte bu belli olmayabilirdi. Bu durumda tepe noktasını grafik denkleminden çıkarmamız gerekir.
Tepe noktası T(r, k) noktası olan bir parabolün denklemi a(x - r)2 + k şeklinde olur. Bu denklemi açtığınız zaman yine ikinci dereceden denklem formu elde edersiniz. Değişen bir şey yok aslında.
Öyleyse örneğimizde y = a(x +1)2 + k denklemini kurabiliriz. Şimdi k değerini bulalım.
Denklemin bilinen kısmını açtığımız zaman ax2 +2ax + 1 + k = y olur.
İkinci dereceden denklemler için yazdığımız ax2 + bx + c formatını hatırlayalım. Denklemde c sabiti y eksenini kesen noktadır demiştir. Bu örnekte k + 1 = c eşitliği vardır. Denklemdeki c değeri -3 olduğuna göre k = -4 olacaktır.
Yani denklemin tepe noktası T(-1, -4) olacaktır.
Denklemle ilgili geride bilmediğimiz sadece a değeri kaldı. Bunu da bilirsek denklemi olduğu gibi elde edebiliriz. Bu değeri elde edebilmek için denklem üzerinde bildiğimiz herhangi bir noktayı yerine yazalım.
Henüz öğrendiğimiz tepe noktasını yazıp görelim. Grafik üstündeki her noktanın denklemi sağlamak zorunda olduğunu unutmayalım.
Denklemde x yerine -1 (r) yazarsak sonucun -4 (k) çıkması gerekecektir.
-4 = a.(-1)2 -2a - 3 â -1 = -a â a =1 bulunur.
Parabolün kolları yukarı doğru olduğu için a değerinin zaten pozitif olması gerekiyordu. Bu değeri 1 olarak bulduk. Şimdi parabolün denklemi ve tepe noktasını biliyoruz.
Parabolün denklemi y = x2 + 2x - 3 olmaktadır. Tepe noktası olan (-1, -4) noktasını yerine yazdığımız zaman da denklem aynen sağlanmaktadır.
Parabol üzerinden başka bir noktayı ele alalım. Parabolün x eksenini kestiği noktalar (-3, 0) ve (1, 0) noktaları da parabol üzerinde olduğu için denklemi aynen sağlayacaktır.
Parabolde Öteleme
Parabol grafiği yukarı-aşağı veya sağa-sola hareket ettirilerek ötelenebilir.
Yukarı Aşağı Öteleme
Bir parabolü sağ ve sol yönde oynatmadan yukarı ya da aşağı kaydırırsanız parabol denkleminin sadece c değeri değişecektir.
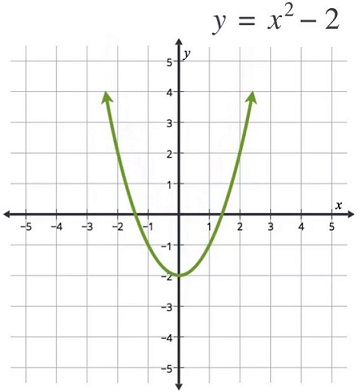
Örneğin yukarıda konuya girerek y = x2 grafiğini vermiştik. Şimdi aşağıdaki y = x2 -2 grafiğine bakın arada iki birimlik bir kayma dışında farkın olmadığını göreceksiniz.
Yukarı aşağı ötelemek denklemde sadece c değerini değiştirir.
Sağa Sola Öteleme
Sağa sola öteleme yaptığımız zaman denklemin kökleri de değişecektir. Burada sadece denklemin sabit c sayısı değil aynı zamanda denklemin içi de değişecektir.
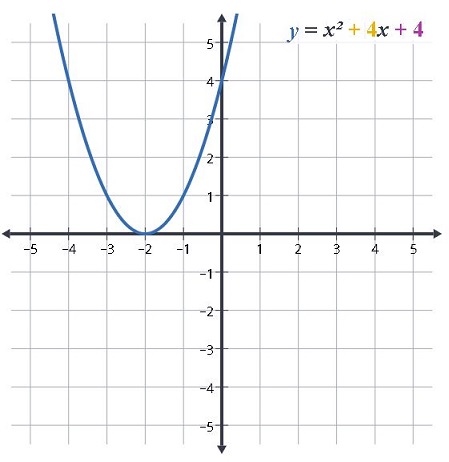
Aynı örnek üzerinden gidecek olursak y = x2 grafiğini iki birim sağa kaydırırsak y = (x + 2)2 grafiği elde edilir. Görüldüğü gibi kareli terimin içi değişmektedir.
Bu durumda elde edilecek yeni denklem grafiği y = x2 + 4x + 4 olacaktır.
Böylece denklemin b ve c değerleri birden değişecektir.
Sağa t birim ötelediğimiz zaman karesi alınan x ifadesi yerine (x - t) yazarız. Sola t birim kadar ötelediğimizde ise (x + t) yazarız.
Baş Katsayı Değişirse
Parabol denklemlerinde baş katsayı x2'nin katsayısı olan a ifadesidir. Bu ifadeyi değiştirmek parabolü ötelemez ancak parabolün yapısını değiştirir.
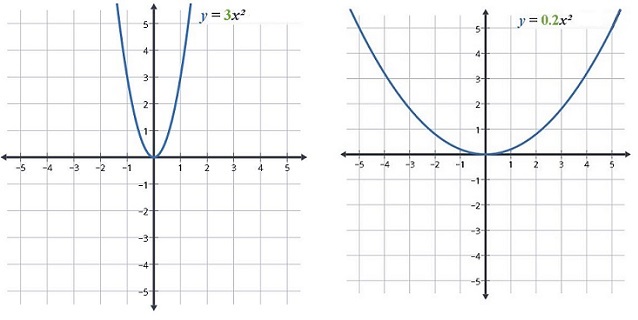
Parabol denkleminde a ifadesi büyüdükçe denklem kolları birbirine daha çok yaklaşır. Tersi de geçerlidir. Kolların genişlemesi için a değerinin küçülmesi gerekir.
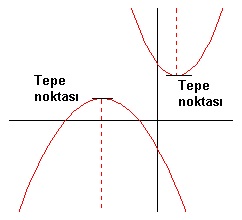
Yukarıdaki örnekte a = 3 ve a = 0.2 için iki adet parabol verilmiştir. Şekil üzerinden karşılaştırma daha net anlaşılabilir.
Eğer baş katsayı negatifse kollar aşağı doğru bakar. Bir parabol denklemini - ile çarpma o denklemin x eksenine göre simetriğini almak demektir.
Parabol Soruları
Parabol konusu için soru çözümü yaparken dikkat edilmesi gerekenler vardır. Her konuda olduğu gibi parabol konusunda da soru çözmek sizin bilgi ve tecrübenizi arttıracaktır.
Parabol sorularını çözerken şu noktalara dikkat edin:
- Baş katsayı için kollar aşağı mı yoksa yukarı mı bakıyor kontrol edin.
- Grafik x eksenine değiyor mu? Değmiyorsa reel sayılarda kök yoktur demektir.
- Grafik y eksenini hangi noktada kesiyor? Kestiği nokta denklemin c değeridir.
Bir parabol sorusu üzerinden öğrendiklerimizi pekiştirelim.
Yukarıdaki soruda parabolün şekli üzerinden değerlendirme yapmamızı istiyor.
Çözüm: Soruyu çözerken yukarıda bahsettiğimiz bilgileri hemen aklımıza getirelim.
- Kollar aşağı olduğuna göre a negatif olur.
- Parabol y eksenini pozitif tarafta kestiğine göre c pozitif olur.
- Tepe noktası pozitif tarafta olduğu için -b/2a da pozitif olmak zorundadır, a negatifse b pozitif olur.
- Sonuç: a negatif, b ve c ise pozitif olur.
Öyleyse A şıkkı için kesin bir şey diyemeyiz. Çünkü bir pozitif ile negatifin toplamının ne olacağını bilemeyiz.
C şıkkında negatif ile pozitifin çarpımı negatif olur yani C şıkkı yanlıştır.
D şıkkında üçünün çarpımı - ile +'ların çarpımından sıfırdan yine küçük olacaktır. Dolayısıyla bu seçenek de yanlıştır.
E şıkkında pozitif - negatif pozitif olacaktır. Bu şık da yanlıştır.
B şıkkında pozitif + pozitif - negatif kesinlik pozitif olacaktır ve 0'dan büyüktür. Öyleyse cevap B seçeneği olur.







 Alıntı ile Cevapla
Alıntı ile Cevapla